上越市が所蔵する江戸時代の歴史資料の中には、意外なほど多くの数学に関する本や帳面、一枚紙の資料等が見つかります。つまり、江戸時代には、想像以上に数学愛好者が多くいたということです。しかし、現代の数学しか知らない私たちにとって、そこに記されている数学問題の題意は理解できても、その解法については理解しにくいものもあります。それは、日本の数学が、江戸時代に独自に目覚ましく発展したからであり、これを「和算」と呼んでいます。
今回は、3月14日が「数学の日」、「円周率の日」であったことにちなみ、和算に関する郷土の歴史資料を、できるだけ数学が苦手な人にも分かるように紹介します。本展示内容の概要を、次の「展示説明資料」に分かりやすくまとめましたので、ご覧ください。
上の「展示説明資料」中の和算問題「油はかり分け算」の解答は、本ページの末尾に載せてありますのでご覧ください。
当センターは、木版印刷で出版された数学書を多数所蔵しています。いくつかを紹介します。
文化12年(1815年)に刊行された「算法點竄指南録(さんぽうてんざんしなんろく)」は、坂部広胖(こうはん)が初学者に点竄術を教授する目的で書いた数学全般についての教科書で、和算史上の名著の一つに数えられています。
「頭書算法闕疑抄(とうしょさんぽうけつぎしょう)」は、奥州二本松藩士の磯村吉徳が「算法闕疑抄」を刊行し、それまでの和算書の集大成と評価されていますが、その増補版で貞享元年(1684年)に出版されています。
「改算塵劫記(かいさんじんこうき)」（安永2年：1773年)は、大ベストセラーであった吉田光由の「塵劫記(じんこうき)」の類書、「改算記大成(かいさんきたいせい)」（元禄9年：1696年）は「塵劫記」に次ぐベストセラーであった山田正重の「改算記」の類書です。
この中から、「算法點竄指南録」の写真を右に載せます。
左の写真は、「算籌明正負記」（吉田祐司家文書）です。これは、小林百哺が校閲した和算書を吉田家が誰かから借り、自学のために書き写したものです。当時の有力な農家や商家等には、印刷された教本以外に、このようにして筆写されたものが多く遺っています。「算籌(さんちゅう)」とは算木のことで、本資料は算木を用いて解く和算の教本、問題集です。例えば、左写真のページには、次のような問題とその解法が記されています。
問題：今有如圖大小方。積和三十四歩、方面差二寸、問小方面幾何。
（意味）今、図のように、大小の正方形がある。面積の和は34歩（ぶ）、一辺の長さの差は2寸（すん）であるとき、小さい正方形の一辺の長さはどれほどか問う。 （1歩は1間四方であり、文脈から、「寸」は「間」の誤写と考えられます。）
答：答曰、小方面三寸。
（意味）答に曰(いわ)く、小正方形一辺は3寸（間）。
解法：術曰、列負一十五个為實、列正二个為法、列正一个為廉而平法開之術小方面合問。
（意味）術に曰く、負数の15を実(じつ：定数項)として置き、正数の2を法(ほう：1次の項）の係数として置き、正数の1を廉(れん：2次の項)の係数として置き、方程式を解くと小正方形の一辺の長さがでる。答えは題意に合っている。
つまり、求める小正方形の一辺の長さをXとすると、（小正方形の面積)＋（大正方形の面積）－34＝0なので、X2＋（X＋2）2－34＝0と立式することができ、これを整理した方程式であるX2＋2X－15＝0を、算木を用いて解く方法が明示されています。 なお、X2はXの2乗を、（X＋2）2は（X＋2）の2乗を表しています。
右の写真は、天明5年(1785年)に作成された「(和算三角法表)」（山田秀紀家文書）です。これは、表の左端の図形（辺の長さが3：4：5の直角三角形とそれに内接する円や正方形からなる図形6種）において、表の各セルが示す長さ相互の比が等しくなるよう意図的に配列されている表です。例えば、表の冒頭は「弦(げん)」（直角三角形の直角に対する辺）：「股(こ)」（直角を挟む長い辺）：「鈎(こう)」（直角を挟む短い辺）となっていますが、これは5：4：3になります。これは当時、「鈎股弦(こうこげん)の定理」（今の「三平方(さんへいほう)の定理」）と呼ばれ、和算では必須で多用されました。
その行の隣は「股」：「長弦」：「中鈎」とありますが、これも5：4：3です。その隣も5：4：3になるという具合に表が作成されています。そして、それをコンパクトにたためるようにし、携帯できるように工夫しています。
下の写真は、慶応2年(1866年)に作成された「見一ヲ八算ニテ割事」（斉藤文雄家文書）です。これには、「見一(けんいち)」（除数が2桁の割り算）を「八算(はっさん)」（除数が1桁の割り算）を用いて計算する方法が示されています。例えば1行目には、「十二ニ割時ハ 二ヲ以テ割、又六ヲ以テ割也」とあります。つまり、12に割るときは「まず2で割り、更に6で割ればよい」と書いてあります。除数が2桁になると難しくなりますが、それを簡単にする工夫です。
「和算當用大全註」：丸田篤家文書(公文書センター所蔵)は、天保9年(1838年)に丸田家が、和算の教本を誰かから借りて書き写し、自学用の冊子にしたものと考えられます。円周率を用いた問題がありましたので、紹介します。
問題：如図円周百廿七間アリ。円積ヲ問フ。 （参考） 1間（けん）＝6尺（しゃく）＝約1.8メートル
（意味）図のように円周が127間の円がある。その円の面積を問う。
答：責(せき)百弐拾七歩六勺（勺は合の書き誤りか） （参考） 1歩（ぶ）＝1間四方＝1坪（つぼ）＝10合（ごう）＝100勺（しゃく）
（意味）面積は、127歩6合
「術(じゅつ)に曰(いわ)く）」として解法が2つ示されています。その2つ目に「円周ヲ三一六ニ約シ円圭ヲ知ル」とあります。これは、「円周を3.16で割り、円の直径を求める」という意味です。つまり江戸時代は、円周率を、私たちが小学校で習った3.14ではなく、3.16で計算していたことが分かります。江戸中期までに3.14の方が正確だと分かった後も、慣習的に3.16を用いたようです。
次いで「自(みずから)シテ得数(えたかず)ニ円法ヲ乗(じょう)シテ責(せき)如答(こたえのごとし)」とあります。これは、「（計算で求めた直径を）自乗(じじょう：2乗)して得た数に円法を乗じて円積は答のようになる」という意味です。「円法」とは円積率のことで、円と外接する正方形の面積を1としたときの円の面積＝0.79を指しています。つまり、「直径×直径×0.79」で円の面積になると言っているわけです。私たちが覚えた公式＝πr2（πr2乗）＝半径×半径×3.14のように半径を基準とするのではなく、江戸時代は直径に着目したようです。
なお、1つ目の解法は、現代の私たちには理解しづらい方法です。「円周百弐拾七間ヲ自シテ壱万六千百廿九歩ニナル。是ヲ実トシテ定法十二六四ヲ法トシテ約シ責如答」とあります。これは、「円周の127(間)を自乗（2乗）して16129歩になる。これを定法の12.64で割って円積は答のようになる」という意味です。確かに16129 ÷12.64＝1276となり、答と一致します。では、12.64なる数字は、どのような意味合いをもつ数字なのでしょうか。
解法の最後に「右定法云々」と、12.64について解説しています。それによれば、「円積率0.79の4倍＝3.16を、更に4倍した数」とあり、確かに0.79×4×4＝12.64となりますが、説明不足のような気がします。
そこで自分なりに考えてみました。江戸時代の円積を求める公式である「直径×直径×0.79＝円積」は、直径＝円周÷3.16なのでそれを代入すると「（円周÷3.16）×（円周÷3.16）×（3.16÷4）＝円積」と表すこともでき、それを整理すると「（円周×円周）÷（3.16×4）＝円積」、つまり「（円周の2乗）÷12.64」となり、まさに解法のとおりです。解法で「定法」と言っているのは、「円周×円周÷12.64＝円積」という公式を用いることを意味していたわけです。
算木は、中国で発明され、奈良時代には日本に伝来していた計算用具です。16世紀後半にそろばんが伝来してからは、加減乗除(かげんじょうじょ)等の簡単な計算はより効率的にできるそろばんで行い、算木は主に複雑な方程式を解くときに用いられました。長さ数センチメートルの角柱で、赤（江村家では白木）で正数を、黒で負数を表します。渡辺慶一収集文書補遺の赤黒の算木（左の写真）は、小林百哺が使ったものと伝わります。
算盤は、算木を用いた計算の補助具です。木製、布製、紙製があり、碁盤目状に格子線が引かれ、上部には一、十、百等と位が書かれています。また、方程式を解くための算盤には、右端の縦列に文字が書いてあり、その意味は、商(しょう)＝答、実(じつ)＝定数項、方(ほう：法とも書く）＝Xの係数、廉(れん)＝X2（Xの2乗）の係数、隅(ぐう：写真では「二乗」）＝X3（Xの3乗）の係数です。
したがって、算木と算盤で、X3＋12X2＋6X－973＝0という方程式は、左の写真のように表します。つまり、X3（Xの3乗）の係数1を赤で「二乗」に置き、X2（Xの2乗）の係数12を赤で「廉」に置き、Xの係数6を赤で「法」に置き、定数項の973を黒で「實」に置きます。
ここで、「おや？」と思われた方もいるでしょう。「X3乗の係数を、なぜ「二乗」に置くの？」という疑問です。実は、江戸時代の何乘というのは、同じ数を何回掛けるという意味なので、例えば「Xの二乘」は和算では 「XにXを2回掛ける」＝X×X×Xで、今日の「X3」（Xの3乗）を意味します。
同様に、何倍は、同じ数を何回加えるという意味なので、「一倍」は「XにXを1回加える」＝X＋Xで今日の二倍を意味し、「人一倍頑張る」は「人より二倍頑張る」という意味です。
しかし、明治になってから西洋数学が主流になり、それに合わせて今日のように表現するようになりました。
「開平」とは平方根(へいほうこん：二乗してその値になる数字）を、「開立」とは立方根(りっぽうこん：三乗してその値になる数字）を求めることで、本資料は、その基本的かつ実用的な問題集です。「二二 八(ににんがはち)」「三三 廿七(さざんにじゅうしち)」などと唱えて覚えるよう「再乗九九(さいじょうくく)」（再乗は意味的には二乗ですが、先述したとおり和算の二乗は今日の三乗です）や、面積から辺の長さを問う問題、利息計算問題等が載っています。
右写真のページは「筭籌(さんちゅう：算木のこと)」の問題で、「米六万八千石(こく)ヲ、六百二十五人ニ分ケ取時(わけとるとき)、一人之(の)取米ヲ問フ 」とあります。算木を使って解法が図示されていますが、625X-68000＝0となるXを求めるよう立式されています。それを解いて、答が「米百〇八石八斗(と)」となります。
そろばんは、伝来当初は度量換算のための16進計算が可能、つまり一桁に15まで置ける上2珠、下5珠の構造でした。日本でも江戸時代は左の写真のとおり、上2珠、下5珠の構造で利用していました。
しかし、上の2球目と下の5球目は不要なことが多く、明治になって上1珠が普及しました。さらに、昭和10年、小学校でそろばんが必修となり、文部省の省令で下4珠に改良されました。その方が、十進位取り記数法にかなうからです。現在では中国でも上1珠、下4珠のそろばんが使用されています。
小林百哺、諱(いみな)は惟孝、通称は祐吉であり、百哺(ももすけ：ひゃっぽ）はその号です。生年月日は明らかではありませんが、五智国分寺境内の碑文に「明治二十年一月九日病歿(びょうぼつ) 年八十四」とありますので、逆算して文化元年（1804年）と考えられます。
幼時から今町の神童と呼ばれ、今町の高良(こうら)鷗隣を師として算学を、府中八幡の月斎から経義(けいぎ)を学びました。高良の没後、門人らは百哺を数学の師としましたが、時に19歳であったそうです。右写真資料「算学門人録」は、百哺20歳のとき以降十数年間の年ごとの入門者名簿であり、牙籌堂(げちゅうどう)とは塾名です。これによれば、この間の新規入門者は総計五百人を超えます。
この間、百哺は27歳、32歳の時に都に上って土御門（安倍）家に入門し、算学のみならず暦学、天文、測量、易学等を学び極めました。また、左写真資料のように、天文数学師として子弟に免状を出すことも許されました。さらに天保14年に3度も上京して司天台(してんだい)師範代になり、弟子は一層増え、遠く信州（長野県）や上州（群馬県）からも集まりました。生涯の門下は五千人余に上るといわれています。
本資料は、いわゆる「見立番付(みたてばんづけ)」です。当時は相撲の番付に擬(ぎ)して、名所旧跡や人物等、様々なテーマでランク付けた一覧表の作成が流行しました。下写真資料は、百哺と、大坂の福田復(ふく)（「美濃正」は通称）という東西和算家の門人をランク付けた一覧です。「司天官(してんかん)」とは、陰陽師(おんみょうじ)：安倍晴明(あべのせいめい)を祖とする土御門晴親(はれちか)のことで、百哺も復もその直弟子で、二人は友人でもありました。
百哺の業績は数学に止まらず、およそ数学を活用する分野には非凡なる才能を示しました。
天保15年（1844年）、海岸防備のため、高田藩は22か所に台場を設けました。その時に測量と台場の設計を藩から命ぜられたのが百哺であり、幕府天文方筆頭の内田五観(いつみ)は「如斯(かくのごとき)難所を能(よ)くもかくまで測量致し候者哉(そうろうものかな)」と驚いています。当センターには、天保2年に妙高山麓で西洋大筒(おおづつ)の「打様(うちため)シ」をする際に百哺が描いた妙高山麓の台場周辺絵図面も遺っています。
慶応元年（1865年）、藩士の砲術指南のために江戸にいた百哺は、そのまま「長州再征」に従軍します。大坂在陣中の宿は、先述した福田復宅であり、この間も百哺に教えを請う者が多数訪れました。また、「戊辰戦争」にも従軍・尽力し、右写真資料の「褒状(ほうじょう)」を得ています。「金三百疋(ひき)」は、小判1枚（一両）の4分の3で、現在の数万円というところでしょう。
ちょっと変わったところで、百哺は家相もみていました。左写真資料は、百哺による「家相判断書」の末尾部分です。家相判断は江戸後期から盛んになり、土御門家の秘伝を授かり、測量や易学、陰陽道にも通じていた百哺の多才が生かされた一例です。
算額については、冒頭の添付ファイル「展示説明資料」に書いたとおりです。五智国分寺の算額については、平丸誠著「頸城の和算家 師石川栄助と弟子野口常保」（1999年）で、明治7年算額の4題、明治32年算額の5題を現代語に書き下し、紹介しています。右写真（提供：村山勝也氏）は、明治32年算額の写真です。掲額された実際の問題は、下の添付ファイルを参照してください。
本資料は、柏崎の閻魔堂(えんまどう)等、県内各所に奉納された算額問題を筆写したものです。その中に、下の写真のように、弘化(こうか)2年（1845年）に、高田の和算家：高橋盈倍の門人が寺町の日朝寺(にっちょうじ)毘沙門堂(びしゃもんどう)に奉納した算額問題（4問：写真はそのうちの3問）の筆写もありました。その中の一つを紹介します。
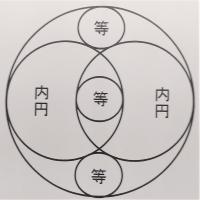問題：外円径若干、問三等円。
（意味）外円の直径が与えられているものとして、3つの等円(の直径)を問う。
解法：術曰五ケ平商ニ乗外円ヲ内減外円二個ヲ余為三等円ト 合問
（意味）5の平方根に外円の直径を掛け、外円直径の二倍を引けば、3等円(の直径)となる。答は題意に合う。
広報記事の筆者：渡辺慶一氏は、上越を代表する郷土史家で、上越を中心とした歴史研究に重要な業績を多数遺しています。当センターも、氏が遺した貴重な歴史資料を多数所蔵しており、それを利用に供しています。
「広報なおえつ」では、小林百哺を、幕末の先覚者：佐久間象山(さくましょうざん)と並べ称し、その業績を伝えています。単に数学に止まらず、天文、暦学、測量、易(えき)学、砲術等、数学を活用する分野全般に精通していたと紹介しています。
「広報じょうえつ」では、小林百哺が、「蛮社の獄(ばんしゃごく)」によって幕府から追われていた蘭学者：高野長英(たかのちょうえい)をかくまうことになった顛末(てんまつ)を詳しく伝えています。長英が自らの命を預けるほど百哺を深く信頼していたこと、百哺に頼まれたとはいえ福永家が本来は取締るべき立場の大肝煎(おおきもいり)でありながら詮議を黙殺して長英を実際に匿ったことが分かります。
問題：1斗桶に油が1斗入っている。7升桝と3升桝を用意して、これを使って5升と5升に分けたい。その方法を述べよ。
（解法） この問題の本質は、2元1次不定方程式の（有理）整数解を求めることにあるそうです。すなわち、7升桝をX回、3升桝をY 回使用して5升を量り取ることにすると、7X＋3Y＝5という2元1次不定方程式ができ、これを解くことになります。
例えば、X＝-1、Y＝4が解として考えられますが、これは3升桝を4回汲み出し、Xの-1は7升桝を1回汲み戻すというように考えるということです。2つの方法を、下に添付ファイルで示します。いずれも5回の操作で完了です。
＜外部リンク＞
PDF形式のファイルをご覧いただく場合には、Adobe社が提供するAcrobat Readerが必要です。
Acrobat Readerをお持ちでない方は、バナーのリンク先からダウンロードしてください。（無料）
〒943-8601 新潟県上越市木田1-1-3電話：025-526-5111Fax：025-526-6111
